Múltiplos e divisores de um número
Um número é múltiplo de outro quando, ao dividirmos o primeiro pelo segundo, o resto é zero. Observe as seguintes divisões entre números Naturais:
As três primeiras divisões têm resto zero. Chamam-se divisões exatas. As duas últimas têm resto diferente de zero. Chamamos de divisão inteira. Um número é divisor do outro se o segundo é múltiplo do primeiro.
O número 10 é múltiplo de 2; 12 é múltiplo de 3; 15 também é múltiplo de 3; mas 9 não é múltiplo de 2; e 15 não é múltiplo de 4.
Vamos agora escrever o conjunto dos múltiplos de 2, indicado por M(2), e dos múltiplos de 5, isto é, M(5):
M(2)={0,2,4,6,8,...}.
M(5) = {0,5,10,15,20,...}
Para lembrar:
O conjunto dos múltiplos de um número Natural não-nulo é infinito e podemos consegui-lo multiplicando-se o número dado por todos os números Naturais. |
Observe:
M(3) = {3 x 0, 3 x 1, 3 x 2, 3 x 3, 3 x 4, 3 x 5, 3 x 6,...} = {0,3,6,9,12,15,18,...}
Observe também que o menor múltiplo de todos os números é sempre o zero. Diremos que um número é divisor de outro se o segundo for múltiplo do primeiro.
No exemplo anterior, observamos que o número 10 é múltiplo de 2, conseqüentemente 2 é divisor de 10.
Os números 12 e 15 são múltiplos de 3, portanto, 3 e 5 são divisores de 12 e 15, respectivamente.Vamos agora escrever o conjunto dos divisores de 15, indicado por D(15), e dos divisores de 20, isto é, D(20):
D(15)={1,3,5,15}
D(20) = {1,2,4,5,10,20}
Observe que o conjunto dos divisores de um número Natural não-nulo é sempre um conjunto finito, em que o menor elemento é o 1 e o maior é o próprio número.
Critérios de divisibilidade
Os critérios de divisibilidade são uma série de regras para averiguar se um número é ou não múltiplo de outro, sem a necessidade de efetuar a divisão de um pelo outro, principalmente quando os números são grandes.
Veja, em seguida, os critérios de divisibilidade mais comuns: Divisibilidade por 2
Olhe para o conjunto dos múltiplos de 2, M(2), exposto acima. Observe que todos os elementos desse conjunto terminam em algarismo par. Assim, podemos dizer que um número é divisível por 2 se o algarismo das unidades for par.
Os números 22, 30, 68, 650, 3 285 416 são múltiplos de 2 porque terminam em algarismo par. Os números 7, 15, 201, 1 483, 186 749 não são múltiplos de 2, pois nenhum deles termina em algarismo par.
Divisibilidade por 3
Observe, agora, o conjunto M(3) = {0,3,6,9,12,15,18,...}. Repare que a soma dos algarismos de todos estes números é múltiplo de 3. Assim, um número é divisível por 3 quando a soma de todos os seus algarismos é múltiplo de 3.
Sem fazer a divisão, vamos comprovar que o número 34 572 é divisível por 3: 3 + 4 + 5 + 7 + 2 = 21, mas pode acontecer de não sabermos se 21 é ou não múltiplo de 3. Repetimos o método agora com o número 21, em que 2 + 1 = 3. Sabemos que 3 é múltiplo de si mesmo, portanto, 21 é divisível por 3, isto é, 21 é múltiplo de 3 e, conseqüentemente, 34 572 é divisível por 3.
Divisibilidade por 5
Observe o algarismo das unidades dos números do conjunto
M(5)={0,5,10,15,20,25,30,35,...}.
É fácil perceber que eles terminam em zero ou em 5. Assim, um número é divisível por 5 quando termina em zero ou em 5.
Os números 20, 210, 2 105 são divisíveis por 5, pois o primeiro e o segundo terminam em zero e o terceiro em 5.
Divisibilidade por 9
Dado M(9) = {0,9,18,27,36,45,...} verificamos uma característica semelhante ao critério de divisibilidade por 3. Um número é divisível por 9 quando a soma de seus algarismos é 9 ou múltiplo de 9.
O número 14 985 é divisível por 9?
Se não soubermos se 27 é ou não múltiplo de 9, repetimos a operação agora com 27:
Portanto, 27 é divisível por 9, isto é, 27 é múltiplo de 9 e, conseqüentemente, 14 985 é divisível por 9.
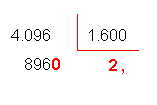
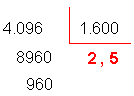
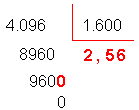O quociente 2,56 é exato, pois o resto é nulo.
.
.
.
